最优化模型 向量和函数

向量是排成一列或一行数字的集合，可以视为n维空间中一个点的坐标。给向量配以加法和标量乘法后，就可以定义独立性、张成空间、子空间和维数等概念。

向量的基本概念

向量是数的集合

向量是一种表示和操作单一数的集合的方法，我们通常把向量写成如下形式：

$$x=\begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix}$$

注意：向量不一定只有二维或三维。例如，可以用一个向量来表示在给定时刻m个机器人的坐标，每个机器人都有坐标$x^{(i)}=(x_1^{(i)},x_2^{(i)})(i=1,···,m).$机器人群位置可以由2m维向量来描述：

$$x=(x_1^{(1)},x_2^{(1)},x_1^{(2)},x_2^{(2)},···,x_1^{(m)},x_2^{(m)})$$

向量空间

向量和与标量乘法

对于向量来说，和、差和标量乘法的运算是以一种显而易见的方式定义的。对于任意两个元素个数相等的向量$v(1),v(2)$，我们定义和$v(1)+v(2)$也是一个向量，他的分量是相加的两个向量的相应分量之和，差也是如此。类似地，如果$v$是向量，$\alpha$是标量，那么将$v$的每个分量乘以$\alpha$，就得到$\alpha v$。如果$\alpha=0$，那么$\alpha v$就是零向量或者原点。

向量空间

从更抽象的角度来看，向量空间$\chi$是通过给向量配备加法和标量乘法运算得到。向量空间的一个简单例子是$\chi=\mathbb{R}^n$，即$n$元实数组的空间；一个不是很显而易见的例子是给定阶数的单变量多项式的集合。

子空间与张成空间

如果向量空间$\chi$有一个非空子集$\nu$，且对任意常数$\alpha,\beta$，有

$$x,y\in\nu\Rightarrow\alpha x+\beta y\in\nu$$

则称向量空间$\nu$为$\chi$的子空间。换句话说，集合$\nu$在加法和标量乘法下是封闭的。注意，子空间总是包含零元素。

向量空间$\chi$上的一个向量集$S={x^{(1)},···,x^{(m)}}$的线性组合为$\alpha_1x^{(1)}+···+\alpha_mx^{(m)}$的形式，其中$\alpha_1,···,\alpha_m$是给定的常数。在$S={x^{(1)},···,x^{(m)}}$中的所有可能向量的线性组合构成的集合是一个子空间，称其为$S$生成的子空间，或者$S$的张成空间，记为$span(S)$。一般地说，由$S$生成的子空间是通过原点的平面。

直和

给定$\mathbb{R}^n$中的两个子空间$\mathcal{X}$和$\mathcal{Y}$，其直和用$\mathcal{X}\oplus \mathcal{Y}$表示，定义是$x+y$形式的向量集，其中$x\in\mathcal{X},y\in \mathcal{Y}$，容易验证$\mathcal{X}\oplus \mathcal{Y}$本身也是一个子空间。

独立性、基和维数

对于向量空间$\chi$中的一列向量$x^{(1)},···,x^{(m)}$，如果其中没有向量可以表示为其他向量的线性组合，则称这列向量是线性独立的。这等价于如下条件：

$$\sum_{i=1}^m\alpha_ix^{(i)}=0\Rightarrow\alpha=0$$

给定向量空间$\chi$中的m个元素构成的集合$S={x^{(1)},···,x^{(m)} }$，考虑由S生成的子空间$\mathcal{S}=span(S)$，即由$S$中向量的所有可能的线性组合构成的集合。假设S中的一个元素$x^{(m)}$可以写成其他元素的线性组合，那么不难发现即使我们从S中删去$x^{(m)}$还是可以得到相同的张成空间，即$span(S)=span(S\setminus x^{(m)})$。可以这样继续下去，直到得到一组向量，比如说$B={x^{(1)},···,x^{(d)}}(d\le m)$使$span(S)=span(B)$，并且这个集合没有元素可以写成集合中其他元素的线性组合（即元素是线性独立的）。这样一个“不可约”集合称为$span(S)$的基，称基中元素个数d为$span(S)$的维数。一个子空间可以有许多不同的基（实际上是无穷多个），但是任何基中的元素个数都是固定的，并且等于子空间的维数。

更一般的说，空间$\mathbb{R}^n$中的标准基为：

$$x^{(1)}=e_1,x^{(2)}=e_2,···,x^{(n)}=e_n,$$

其中$e_i$表示$\mathbb{R}^n$中的一个向量，它的第$i$个分量为1，其他分量都是0。

仿射集

仿射集是一个与子空间相关的概念，仿射集被定义为子空间的平移。也就是说，仿射集是如下形式的集合：

$$\mathcal{A}=\{x\in\mathcal{X}:\ x=v+x^{(0)},v\in\mathcal{V}\},$$

其中$x^{(0)}$为给定的点，$\mathcal{V}$为给定的$\mathcal{X}$的一个子空间。子空间是包含原点的仿射集。

范数与内积

欧氏长度与$\mathcal{l}_p$范数

长度与距离的概念

向量$x\in \mathbb{R}^n$的欧氏长度是$x$各分量平方和的平方根。这个公式对二维情形下毕达哥斯拉定理在多维情况下的一个明显拓展。欧氏长度表示从原点O开始，沿着最直接的路径到达点$x$的实际距离。

然而，除了欧氏空间之外，对向量空间中的长度和距离有一个稍微更一般的概念。假设从O到$x$我们不能沿着直线路径移动，必须沿着一个正交网格走，在这种情况下，从0到$x$的最短距离由$x$的分量绝对值之和给出：

$$x的长度(沿正交网格)=|x_1|+|x_2|+···+|x_n|.$$

范数与$\mathcal{l}_p$范数

向量空间$\mathcal{X}$上的范数是将任意元素$x\in\mathcal{X}$映射成实数$||x||$的具有特殊性质的实质函数。范数就是一个映射，它将一个$n$维向量变成实数。

$$\begin{alignat*}{1} 定义\ &若\mathcal{X}到\mathbb{R}的一个函数满足如下条件\\ &||x||\geqslant0，\forall x\in\mathcal{X}且||x||=0当且仅当x=0;\\ &||x+y||\le||x||+||y||，\forall x,y\in\mathcal{X}(三角不等式);\\ &对任意标量\alpha和x\in\mathcal{X}，有||\alpha x||=|\alpha|||x||.\\ &则称这个函数为范数。 \end{alignat*}$$

向量空间$\mathcal{X}=\mathbb{R}^n$上的范数的例子包括所谓的$\mathcal{l}_p$范数，其定义如下：

$$||x||_p\doteq(\sum_{k=1}^n|x_k|^p)^{\frac{1}{p}},\ 1\le p\le\infty$$

特别地，当$p=2$时，我们得到标准地欧氏长度：

$$||x||_2\doteq\sqrt{\sum_{k=1}^n|x_k|^2},$$

当$p=1$时，可以得到绝对值和表示的长度：

$$||x||_1\doteq\sum_{k=1}^n|x_k|,$$

极限情形$p=\infty$则定义了$\mathcal{l}_\infty$范数（最大绝对值范数或切比雪夫范数）

$$||x||_\infty\doteq\max_{k=1,···,n}|x_k|,$$

单位球

称$\mathcal{l}_p$范数小于等于1的所有向量构成的集合

$$\mathcal{B}_p=\{x\in\mathbb{R}^n:\ ||x||_o\le1\}$$

为$\mathcal{l}_p$范数的单位球。依赖于不同的$p$值，集合$\mathcal{B}_p$有不同的集合形状。

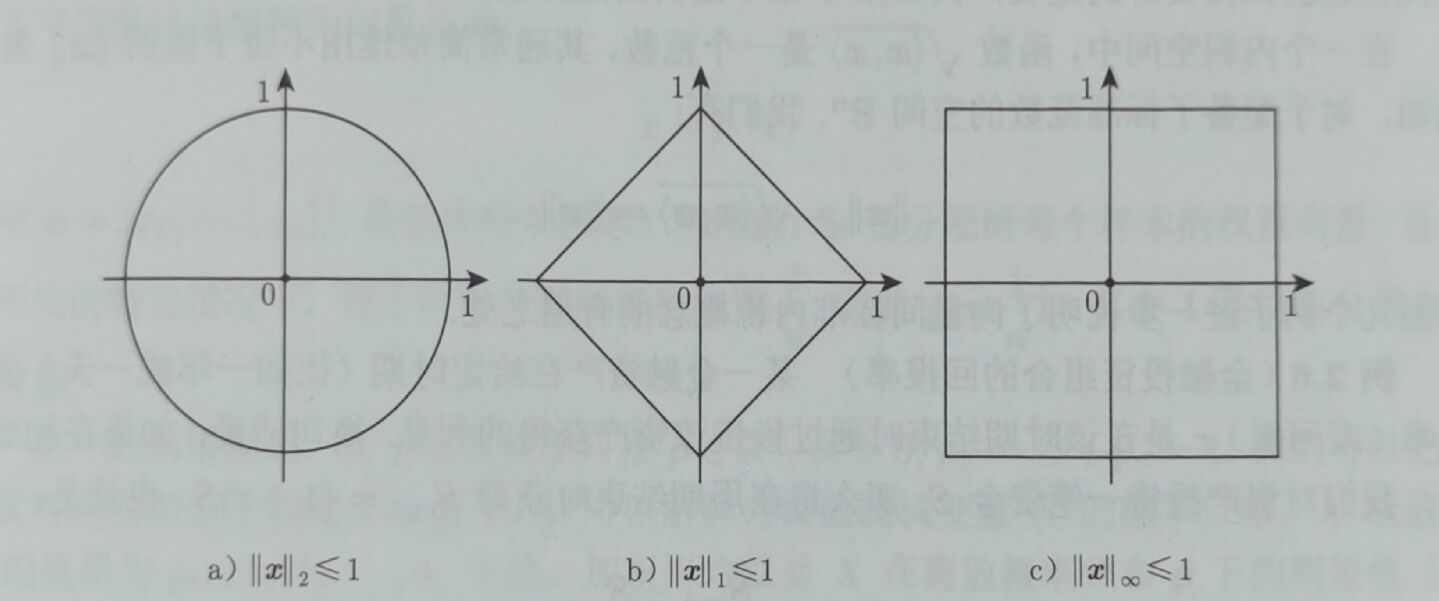
$\mathcal{l}2$范数的单位圆，$\sqrt{x^2+y^2}=1$是圆；$\mathcal{l}_1$范数的单位圆，$|x|+|y|=1$是菱形，边上每个点的横纵坐标距离之和为1；$\mathcal{l}\infty$范数的单位圆，$\max{|x|,|y|}=1$是正方形，边上每个点的横纵坐标最大值为1。

我们观察到$\mathcal{l}_2$范数不“偏向”空间中的任何方向，即它是旋转不变的，这意味着任意旋转的定长向量将保持相同的$\mathcal{l}_2$范数。反之，同一向量会有不同的$\mathcal{l}_1$范数，当其与坐标轴对其时，达到最小值。

内积、角度和正交性

内积

$$\begin{alignat*}{1} 定义：\ &向量空间\mathcal{X}上的内积是一个实值函数，它将任意一对元素x,y\in\mathcal{X}映射成标量，记为<x,y>.内积满足以下公理：对于任意x,y,z\in\mathcal{X}和标量\alpha，有\\ &<x,y>\geqslant 0;\\ &<x,x>=0当且仅当x=0;\\ &<x+y,z>=<x,z>+<y,z>;\\ &<\alpha x,y>=\alpha <x,y>;\\ &<x,y>=<y,x> \end{alignat*}$$

称配有内积的向量空间为内积空间。

空间$\mathbb{R}^n$上定义的标准内积为两个向量的“行—列”乘积：

$$<x,y>=x^\top y=\sum_{k=1}^nx_ky_k$$

在一个内积空间中，函数$\sqrt{}$是一个范数，其通常简单地用不带下标地$||x||$表示。例如，对于配备了标准范数地空间$\mathbb{R}^n$，我们有：

$$||x||=\sqrt{<x,x>}=||x||_2$$

向量间的角度

若将两个非零向量$x,y$视为笛卡尔空间的两点，可以考虑$x,y$与原点O构成的三角形，设$\theta$为三角形$Ox$和$Oy$边之间的夹角以及$z=x-y$，则我们有：

$$\begin{alignat*}{1} ||z||_2^2&=(||y||_2\sin \theta)^2+(||x||_2-||y||_2\cos \theta)^2\\ &=||x||_2^2+||y||_2^2-2||x||_2||y||_2\cos \theta \end{alignat*}$$

而

$$||z||_2^2=||x-y||_2^2=(x-y)^\top(x-y)=x^\top x+y^\top y-2x^\top y,$$

结合上两式得：

$$||x||_2||y||_2\cos \theta=x^\top y$$

由此可得$x$和$y$之间的角度定义为：

$$\cos \theta=\frac{x^\top y}{||x||_2||y||_2}$$

柯西—施瓦茨不等式及其推广

因为$|\cos\theta|\le1$，那么由上式可以得到：

$$|x^\top y|\le||x||_2||y||_2$$

该不等式的一个推广设计常见的$\mathcal{l}_p$范数，并被称为$H\ddot{o}lder$不等式，对于任意向量$x,y\in\mathbb{R}^n$以及任意$p,q\geqslant1$满足$\frac{1}{p}+\frac{1}{q}=1$，如下不等式成立：

$$|x^\top y|\le\sum_{k=1}^n|x_ky_k|\le||x||_p||y||_q.$$

范数球上的内积最大化

给定一个非零向量$y\in\mathbb{R}^n$，考虑寻找某个向量$x\in\mathcal{B}_p(\mathcal{l}_p范数下的单位球)$是的内积$x^\top y$达到最大值的问题，也就是求解

$$\max_{||x||_p\le1}x^\top y.$$

对于$p=2$，该解很容易由前式得到：要求$x$和$y$平行以形成一个零度角，从而有可能最大的范数，即对应范数等于1.于是，唯一的解为：$x_2^*=\frac{y}{||y||_2}$。

这样则有$\max_{||x||_2\le1}x^\top y=||y||_2.$

下面考虑$p=\infty$的情形。由于$x^\top y=\sum{i=1}^nx_iy_i$，其中每个$x_i$都满足$|x_i|\le1$，那么当取$x_i=sgn(y_i)$时（$sgn$表示符号函数，按照定义，当$x>0$时$sgn(x)=1$,当$x<0$时$sgn(x)=-1$，而当$x=0$时，$sgn(x)=0$），即$x_iy_i=|y_i|$，该求和达到最大值。因此有：$x\infty^*=sgn(y)$.

以及$\max{||x||\infty\le1}x^\top y=\sum_{i=1}^n|y_i|=||y||_1.$最优解可能不是唯一的，因为当$y_i=0$时，可以任意选取$x\in[-1,1]$。

最后，考虑$p=1$的情况。内积$x^\top y=\sum_{i=1}^nx_iy_i$现在可以解释为$y_i$的加权平均值，其中$x_i$是权重，其绝对值之和必须等于1。加权平均值的最大值是通过找到具有最大绝对值的$y_i$，即通过找到一个索引指标$m$使对所有$i=1,···,n,$都有$|y_i|\le|y_m|$，然后令

$$[x_1^*]_i= \left\{ \begin{array}{lc} sgn(y_i)&i=m\\ 0&其他\\ \end{array} \right.,i=1,···,n.$$

这样就得到$\max{||x||_1\le1}x^\top y=\max_i|y_i|=||y||\infty.$同样，最优解可能也不是唯一的，这是因为在向量$y$有几个具有相同最大绝对值的分量的情况下，可以选择$m$为这其中任意一个分量的下标。

正交与正交补

如果$\mathcal{X}$中的两个向量$x,y$有$=0$，则称$x$和$y$是正交的。

正交向量

将正交的概念推广到一般内积空间，如果内积空间$\mathcal{X}$中的两个向量$x,y$有$=0$，则称$x$和$y$是正交的。用$x\bot y$来表示两个向量$x,y\in\mathcal{X}$是正交的。

正交向量集

若一簇向量构成的集合$S={x^{(1)},···,x^{(d)}}$满足，对于$i,j=1,···,d,$有

$$<x^{(i)},x^{(j)}>= \left\{ \begin{array}{lc} 1&i\not=j,\\ 0&i=j.\\ \end{array} \right.$$

则称集合S是正交的。换句话说，如果每个向量范数都为1，并且所有向量都相互正交，那么S就是正交的，正交向量集S构成了S张成空间的一组正交基。

正交补

设向量$x\in\mathcal{X}$，且$\mathcal{S}$是内积空间的子集，如果对所有$\mathcal{s}\in\mathcal{S}$，都有$x\bot\mathcal{s}$，那么称向量$x$与$\mathcal{S}$正交。空间$\mathcal{X}$中所有与$\mathcal{S}$正交的向量构成的集合成为$\mathcal{S}$的正交补，用$\mathcal{S}^\bot$表示。